Crystal Systems and Crystal Structure
Crystal Structure
Crystal structure refers to the orderly, repeating arrangement of atoms, ions, or molecules in a crystalline material. This arrangement defines the shape, symmetry, and properties of the crystal, influencing characteristics like strength, electrical conductivity, thermal conductivity, and optical properties. Understanding crystal structures is crucial across chemistry, physics, materials science, and engineering because the arrangement of particles greatly affects the material’s overall properties.
Key Concepts of Crystal Structure
1. Unit Cell
The unit cell is the smallest repeating unit in a crystal. Acting as the "building block" of the crystal, it contains atoms or molecules in a specific, orderly pattern. Repeating this unit cell in three dimensions forms the entire crystal lattice. Key characteristics of a unit cell include:
2. Crystal Lattice
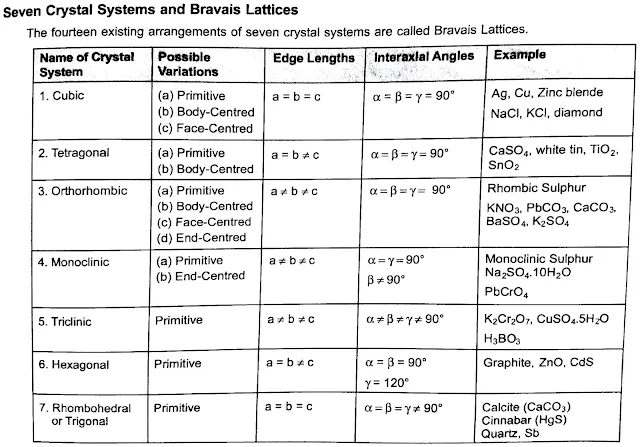
The crystal lattice is a three-dimensional grid where each point represents the position of a unit cell. This lattice creates an organized pattern through space, with lattice points that indicate where atoms or ions repeat. The French crystallographer Auguste Bravais identified 14 distinct types of crystal lattices, now known as Bravais lattices. These types describe different symmetrical arrangements of unit cells.
3. Lattice Points
Each lattice point represents an atom or group of atoms that repeats in space, defining the crystal’s symmetry and unique structure. Lattice points form a repetitive pattern, resulting in a lattice that helps establish the crystal's internal structure.
Translational Symmetry and Lattices
A lattice is an ordered array generated by translating a single motif across space. The smallest repeating unit within a lattice, called the unit cell, replicates in all three dimensions to form the full lattice. In crystallography, unit cell corners are designated as lattice points, and these points connect in a way that delineates the unit cell boundaries (or crystallographic axes).
Types of Planar and Three-Dimensional Lattices
In two-dimensional space, only five types of lattices exist:
- Square
- Rectangular
- Centered rectangular
- Parallelogram
- Hexagonal
In three-dimensional space, only 14 unique lattices are possible, known as Bravais lattices. These types account for different unit cell shapes and arrangements, from simple cubes to complex hexagonal structures.
Symmetry in Crystal Structures
Symmetry is a central feature of crystal structures. It describes the periodic repetition of structural features, contributing to the crystal’s overall form and classification. There are two main types of symmetry:
Translational Symmetry: Repeats a motif (basic repeating unit) across a specific length, area, or volume.
Point Symmetry: Repeats a motif around a central point. Key point symmetry operations include:
- Reflection: Mirror-image symmetry across a plane.
- Rotation: Repetition of a motif after rotating it by a fixed angle.
- Inversion: A motif’s reflection across a center point in the crystal.
- Rotoinversion: Combines rotation and inversion for complex symmetry.
Crystal Classes and Systems
Different combinations of symmetry operations categorize crystals into 32 distinct crystal classes. These classes are grouped into six crystal systems (e.g., cubic, hexagonal, tetragonal), each system based on a unique symmetry characteristic.
Crystal Forms
A crystal form is defined by a set of faces that are geometrically equivalent and related by symmetry operations. Simple crystals may consist of only one crystal form, while complex ones may combine multiple forms. In the isometric system, 15 different crystal forms are possible, such as prisms, pyramids, and dipyramids.
Importance and Applications of Crystal Structures
The internal arrangement of atoms within a crystal structure determines properties like:
Mechanical Strength: Close-packed structures are generally strong, whereas open structures can be more brittle.
Electrical Conductivity: Highly symmetrical and closely packed structures like metals (FCC and BCC) have high electrical conductivity due to free electron movement.
Optical Properties: The crystal’s arrangement affects how light passes through it, impacting properties like transparency and color.
Thermal Conductivity: Simple, close-packed structures usually conduct heat well because of efficient vibrational energy transfer.
These properties make crystal structures essential for various applications, including material design, pharmaceuticals, electronics, and mineralogy.
 |
| Crystal Systems and Crystal Structure |
Crystal Systems
Crystal systems are a way of classifying crystals based on the symmetry of their unit cells. The unit cell is the smallest repeating unit of a crystal structure.
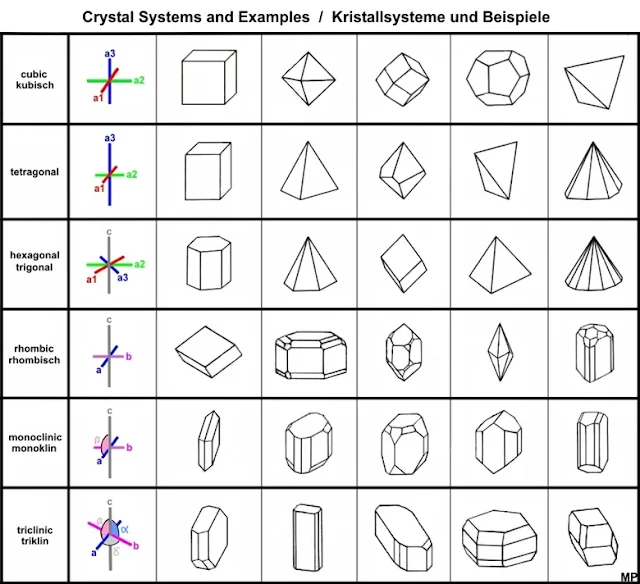
Every crystal class is a member of one of the seven crystal systems. These systems include the isometric, hexagonal, Trigonal, tetragonal, orthorhombic, monoclinic, and triclinic crystal systems.
Every crystal class which belongs to a certain crystal system will share a characteristic symmetry element with the other members of its system. For example, all crystals of the isometric system possess four 3-fold axes of symmetry which proceed diagonally from corner to corner through the center of the cubic unit cell. In contrast, all crystals of the hexagonal division of the hexagonal system possess a single six-fold axis of rotation.
The crystal system of a mineral species may sometimes be determined in the field by visually examining a particularly well-formed crystal of the species.
Isometric Crystal System
The isometric crystal system is also known as the cubic system. The crystallographic axes used in this system are of equal length and are mutually perpendicular, occurring at right angles to one another.All crystals of the isometric system possess four 3-fold axes of symmetry, each of which proceeds diagonally from corner to corner through the center of the cubic unit cell.
Hexagonal Crystal System
The hexagonal crystal system is defined by its unique lattice structure, characterized by four crystallographic axes. Three of these axes (a₁, a₂, and a₃) are of equal length and lie in the same plane, intersecting each other at 120° angles. The fourth axis, known as the c-axis, is perpendicular to this plane and is typically of a different length, either longer or shorter than the other three. The unit cell of a hexagonal crystal is often depicted as a hexagonal prism, with the parameters "a" representing the length of the three equal axes and "c" representing the length of the perpendicular axis.
In terms of symmetry, the hexagonal system is known for its six-fold rotational symmetry. This means that rotating the crystal by 60° (or multiples of 60°) around the c-axis will yield an identical appearance. This system also often includes multiple reflection planes, which contribute to the symmetrical and visually appealing nature of hexagonal crystals. Common examples of minerals that crystallize in the hexagonal system include quartz, which is one of the most abundant and well-known minerals, and beryl, which forms gemstones like emerald and aquamarine.
Minerals like quartz and beryl are well-known examples of crystals that
form in the hexagonal system, often producing large, visually striking
prismatic crystals.
Trigonal Crystal System
The trigonal system can be considered a subset of the hexagonal system. Both systems share a similar lattice structure, but the key difference lies in the symmetry. Hexagonal crystals have six-fold rotational symmetry, while trigonal crystals have three-fold rotational symmetry.
Minerals like calcite and tourmaline, which crystallize in the trigonal system, typically form rhombohedral or scalenohedral shapes that reflect this lower symmetry.
Tetragonal Crystal System
Minerals of the tetragonal crystal system are referred to three mutually perpendicular axes. The two horizontal axes are of equal length, while the vertical axis is of different length and may be either shorter or longer than the other two.Minerals of this system all possess a single 4-fold symmetry axis. They may possess up to four 2-fold axes of rotation, a center of inversion, and up to five mirror planes.
Mineral examples which crystallize in the tetragonal crystal system are zircon and cassiterite. These minerals tend to produce short crystals of prismatic habit.
Orthorhombic Crystal System
Minerals of the orthorhombic crystal system are referred to three mutually perpendicular axes, each of which is of a different length than the others. Crystals of this system uniformly possess three 2-fold rotation axes and/or three mirror planes.The holomorphic class demonstrates three 2-fold symmetry axes and three mirror planes as well as a center of inversion. Other classes may demonstrate three 2-fold axes of rotation or one 2-fold rotation axis and two mirror planes.
Monoclinic Crystal System
Crystals of the monoclinic system are referred to three unequal axes. Two of these axes are inclined toward each other at an oblique angle; these are usually depicted vertically. The third axis is perpendicular to the other two. The two vertical axes therefore do not intersect one another at right angles, although both are perpendicular to the horizontal axis.Monoclinic crystals demonstrate a single 2-fold rotation axis and/or a single mirror plane. The holomorphic class possesses the single 2-fold rotation axis, a mirror plane, and a center of symmetry. Other classes display just the 2-fold rotation axis or just the mirror plane.
Mineral examples which adhere to the monoclinic crystal system include pyroxene, amphibole, orthoclase, azurite, and malachite, among many others. The minerals of the monoclinic system tend to produce long prisms.













%20(1).webp)